Der herausragende Mathematiker des Mittelalters Leonardo da Pisa (Fibonacci - Sohn des Bonacci), hat die arabischen Zahlen eingeführt. Dadurch wurde das alte römische Zahlensystem verdrängt.
Wer war Leonardo Fibonacci?
Leonardo Fibonacci, oder eigentlich Leonardo Bonacci, auch bekannt als Leonardo von Pisa, war ein italienischer Mathematiker, der von etwa 1170 bis etwa 1250 lebte. Er gilt als der begabteste westliche Mathematiker des Mittelalters. Der junge Fibonacci wurde in Afrika erzogen, weil sein Vater, ein Diplomat, eine diplomatische Mission in Nordafrika hatte. Fibonacci reiste unter anderem nach Ägypten, Syrien, in die Provence, nach Griechenland und Sizilien.
Auf seinen Reisen durch Europa und den Osten lernte er die Errungenschaften der arabischen und indischen Mathematiker kennen - darunter auch das Dezimalsystem. Er schrieb viele Werke, von denen ein Großteil leider verloren gingen. Fibonaccis bekannteste Veröffentlichungen sind das bereits erwähnte Liber Abaci von 1202, Practica Geometriae von 1220, Flos von 1225 sowie das verlorene Di minor guisa.

Die bekannte Fibonacci-Zahlenreihe
Wir werden später in diesem Artikel auf die Funktionsweise der einzelnen Systeme eingehen. Alle Fibonacci-Techniken basieren auf der so genannten Fibonacci-Zahlenreihe, einer Zahlenfolge natürlicher Zahlen, die wie folgt von Leonardo definiert wurde:
- die erste Zahl ist 0
- die zweite Zahl ist 1
- jede weitere Zahl ist die Summe der beiden vorhergehenden Zahlen:
z.B. 1+1=2 / 1+2=3 / 2+3=5 / 3+5=8
Auf diese Weise erhält man eine unendliche Zahlenfolge:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, usw.
Die Fibonacci-Zahlenreihe wurde von Fibonacci in seinem Werk "Liber Abaci" im Jahr 1202 beschrieben. Sie existiert unter dem Namen Fibonacci-Zahlenreihe seit dem 19. Jahrhundert, als sie von dem französischen Mathematiker Édouard Lucas populär gemacht wurde.
Die Fibonacci-Zahlen sind eng mit der sogenannten goldenen Mitte verbunden, die auch als der "Goldene Schnitt" bezeichnet wird. Die Besonderheit besteht darin, dass ein Segment so geteilt wird, dass das Verhältnis des längeren Teils des Segments zum kürzeren Teil gleich dem Verhältnis des gesamten Segments zum längeren Teil ist. Damit so ein Verhältnis besteht, muss die Länge des längeren Teils des Segments das geometrische Mittel der Längen des kürzeren Teils des Segments und des gesamten Segments sein.
Das Verhältnis zwischen den Quotienten zweier aufeinanderfolgender Zahlen der Fibonacci-Zahlenreihe ist eine Annäherung an die Goldene Zahl. Diese Beziehungen kommen in der Natur vor und werden auch in der Malerei (Leonardo da Vinci), in der Architektur (z.B. das Pantheon in Rom), in der Musik und auf den Finanzmärkten genutzt.

Die Fibonacci-Ratios - das Maß aller Dinge
Wir haben bereits festgestellt, dass die Fibonacci-Zahlenreihe eine unendliche Folge von Zahlen ist, die mit den Werten 0 und 1 beginnt und mit den Zahlen fortgesetzt wird, die die Summe der beiden vorhergehenden Werte sind, was die Folge 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 usw. ergibt. Es gibt interessante Beziehungen zwischen aufeinanderfolgenden Zahlen der Reihe, die auch als der bereits erwähnte Goldene Schnitt bekannt ist.
Teilt man eine beliebige Zahl der Folge durch die vorhergehende, erhält man einen Wert, der um 1,61804 schwankt. Dies ist der in der Geometrie bekannte Goldene Schnitt, der mit dem einundzwanzigsten Buchstaben des griechischen Alphabets - phi (φ oder ϕ) - bezeichnet wird. Je größer die Zahlen sind, die wir dividieren, desto näher kommt das Ergebnis dem Goldenen Schnitt.
Als Ergebnis einiger grundlegender Berechnungen erhalten wir die folgenden Fibonacci-Ratios, die für Fibonacci-Techniken verwendet werden:
1/1,618 = 0,618;
0,618 * 0,618 = 0,382;
1,618 * 1,618 = 2,618;
2,618 * 1,618 = 4,236;
1 /1,618^2 = 0,282
Es gibt auch Händler, die neben den Niveaus von 0,382, 0,618, 2,618 und 4,236 auch das Niveau von 1,272, das sich aus der Quadratwurzel aus 1,618 ergibt, und das Niveau von 0,786, das die Quadratwurzel aus dem Quotienten von 1 /1,618 ist, verwenden. Zusätzlich zu den Fibonacci-Ratios wird eine Zahl von 0,50 an die Fibonacci-Ratios angehängt, da als Faustregel angenommen wird, dass das Niveau in der Mitte der Bewegung in der technischen Analyse von analytischer Bedeutung ist.
Weitere Koeffizienten sind noch 0,886, die Quadratwurzel aus 0,786 (sowie die vierte Wurzel aus 0,618), und 1,13, die Umkehrung von 0,886. Es gibt noch mehrere andere Koeffizienten, so dass eine Unterteilung in Hauptkoeffizienten, Koeffizienten, die sich aus grundlegenden Aktionen auf Hauptkoeffizienten ergeben, und zusätzliche Koeffizienten vorgenommen wird.
Die Methode zur Messung der Kursbewegungen mit Hilfe der Fibonacci-Ratios beruht auf der Annahme, dass die oben genannten goldenen Verhältnisse, die in der Natur vorkommen, sowie auf den Kurscharts von Finanzinstrumenten erscheinen. In jedem Zeitrahmen auf den Märkten bei Aktien, Futures, Anleihen, Währungen usw. Natürlich sind die Meinungen über diese Methode geteilt, wie es bei technischen Analyseinstrumenten üblich ist.
Die Fibonacci-Werkzeuge für die Börse
Es gibt sechs Fibonacci-Werkzeuge,für den Handel an der Börse, die auf den meisten Handelsplattformen verfügbar sind. Diese Werkzeuge sind unterschiedlich, aber sie basieren alle auf der Fibonacci-Zahlenreihe und den Verhältnissen zwischen den aufeinanderfolgenden Zahlen der Zahlenreihe. Das beliebteste der sechs Werkzeuge ist das Fibonacci-Retracement.
Auf TradingView oder auf dem MetaTrader 4 oder 5 beispielsweise finden Sie sie unter der Kategorie Fibonacci-Werkzeuge.
Die sechs Techniken, die auf Fibonacci basieren, sind:
- Fibonacci-Retracement
- Fibonacci-Extensions
- Fibonacci-Kanäle
- Fibonacci-Zeitzonen (Timezones)
- Fibonacci-Bögen (Arcs)
- Fibonacci-Fächer (Fan)
Die Integration der Fibonacci-Methoden in Ihre Handelsstrategien ist sehr arbeitsintensiv, da es viel Erfahrung erfordert, sie richtig auf einem Kurschart darzustellen. Es reicht nicht aus, einfach die Parameter einzustellen und sie auf ein Chart zu werfen, wie es bei den meisten Indikatoren und Oszillatoren der Fall ist.
Sie müssen eigentliche mit Tests auf einem Demokonto beginnen. Dann entscheiden Sie, welches Fibonacci-Werkzeug am besten zu Ihnen passt. Ob Sie sich mehr auf die letzte Bewegung oder auf den gesamten Kursverlauf, auf die Stärke des vorherrschenden Trend oder auf die Dauer einer bestimmten Situation konzentrieren wollen. Natürlich können Sie Ihre Meinung später immer noch ändern, aber Sie sind gut beraten, wenn Sie sich darüber im Klaren sind, was am besten zu Ihrem Handelssystem passt.
Fibonacci-Retracement
Diese Methode wird jedoch von einem breiten Spektrum von Anlegern genutzt, was ihre Wirksamkeit erhöht. Die einfachste Anwendung der Fibonacci-Retracement besteht darin, das letzte signifikante Hoch und Tief auf einem Kurschart zu bestimmen. Das Problem könnte darin bestehen, dass die Bestimmung dieser Extremwerte recht willkürlich ist und besondere Schwierigkeiten bei Konsolidierungen auftreten können (bei einem starken Trend dürfte die Bestimmung der letzten Extremwerte keine schwierige Aufgabe sein).
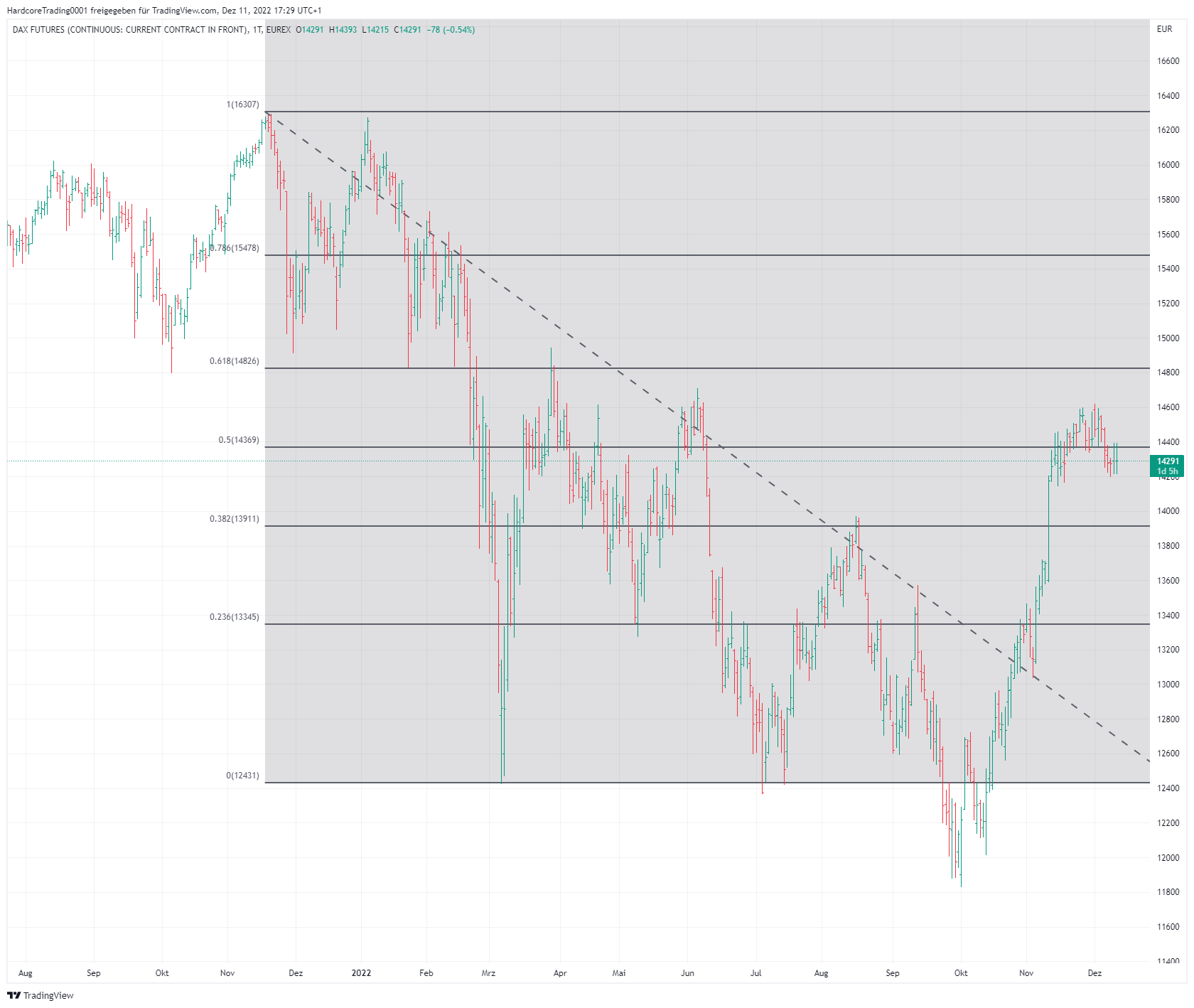
Die absolute Differenz zwischen den ermittelten Extremen ist der sogenannte Einheitsquerschnitt. Dieser Abschnitt wird dann in Proportionen unterteilt, die Fibonacci-Verhältnisse sind und durch Fibo-Verhältnisse größer als eins erweitert werden. Diese Niveaus gelten als wichtige Unterstützungs- und Widerstandszonen für das jeweilige Finanzinstrument.
Fibonacci-Extensions
Die Fibonacci-Extensions (Expansion) ist den Fibonacci-Ratios sehr ähnlich. Er wird verwendet, um die theoretischen Endpunkte der Fortsetzung einer Bewegung nach einer Korrektur zu bestimmen. Damit misst man also nicht nur die letzte Bewegung, wie bei den Fibonacci-Retracement, sondern die letzten beiden Bewegungen des Trends und der Korrektur. Durch die Messung des Trends, einschließlich der Korrekturbewegung, können wir die Niveaus bestimmen, auf denen die nächste Korrektur oder der nächste Trendwechsel stattfinden kann. Die grundlegenden Expansionsstufen sind die 61,8 %-, 100 %- und 161,8 %-Grenze.
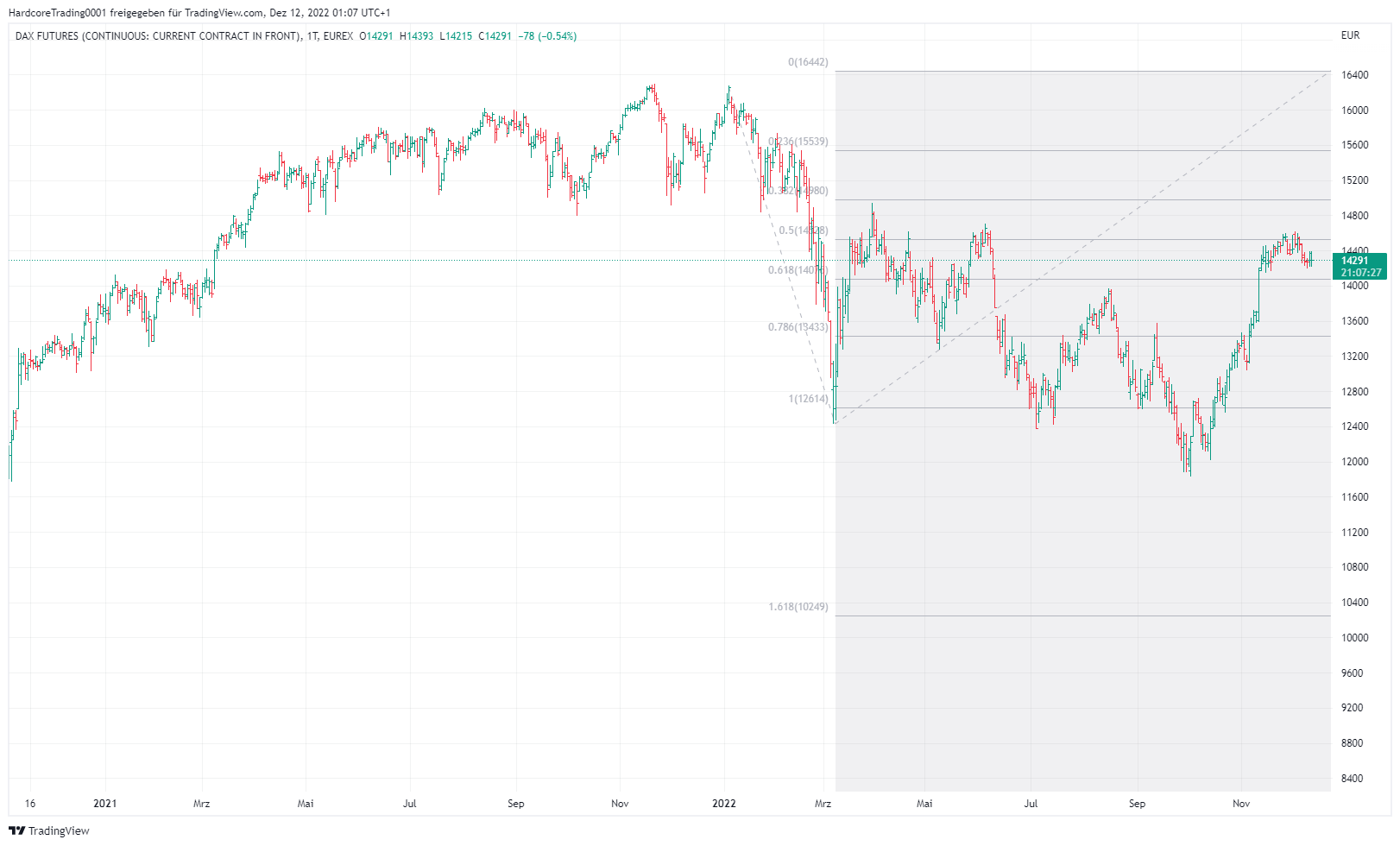
Fibonacci-Zeitzonen (Timezones)
Fibonacci-Zyklen oder Fibo-Zeitzonen sind um 90 Grad gedrehte Fibonacci-Ebenen - sie führen uns von der Preisachse zur Zeitachse. Sie werden auch verwendet, um potenzielle Wendepunkte auf dem Diagramm zu bestimmen, allerdings nicht aufgrund der Stärke und Richtung der Kursbewegungen, sondern aufgrund ihrer Dauer. Dieses Instrument misst also, wie lange es gedauert hat, bis sich die letzte Welle gebildet hat, und bestimmt auf dieser Grundlage den Punkt, an dem die nächste Bewegung enden sollte.
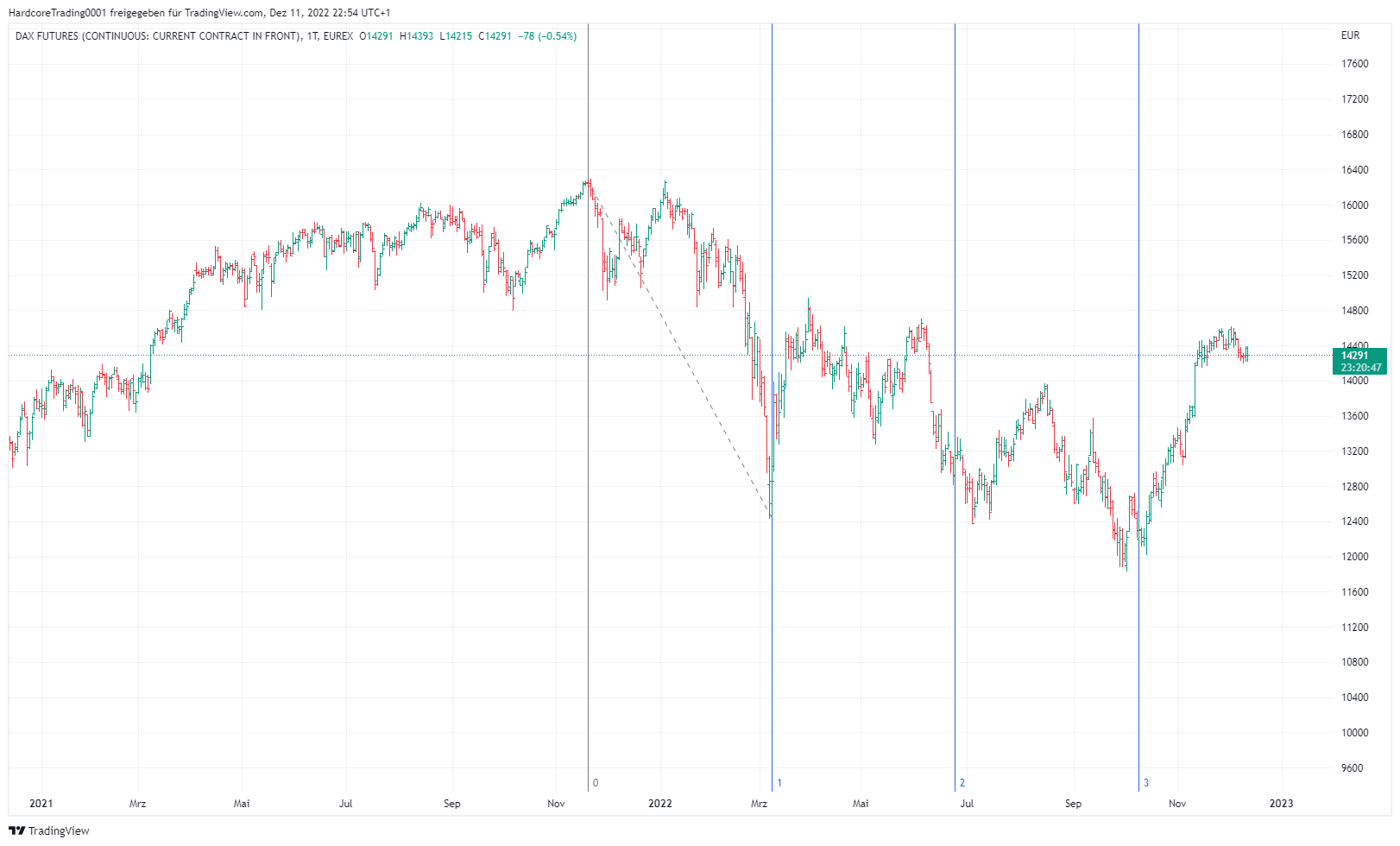
Fibonacci-Kanäle
Fibonacci-Kanäle sind einfache Preiskanäle, die auf Fibonacci-Verhältnissen basieren und sich parallel zum Trendkanal ausrichten. Dieses Instrument eignet sich daher für den Einsatz bei einer stabilen und lang anhaltenden Kursbewegung, bei der Sie klare parallele Trendlinien erkennen können, die sowohl entlang der Tiefst- als auch der Höchststände dieses Trends verlaufen. Mit ihrer Hilfe lassen sich aufeinander folgende Kanäle identifizieren, in denen sich der Kurs nach einer Änderung der Bewegungsstärke bewegen kann.
Fibonacci-Kanäle werden entlang des aktuellen Trends gezeichnet. Vorausgesetzt wird, dass sich der Kurs in einem klaren Trend bewegt. Mit dem ersten Klick stellen wir den Winkel des Kanals ein und mit der zweiten, parallelen Linie legen wir die Breite des konstruierten Kanals fest. So muss eine Linie den aufeinanderfolgenden Höchstständen und die andere Linie den aufeinanderfolgenden Tiefstständen folgen. Oben finden Sie ein Beispiel für die Festlegung eines Fibonacci-Kurskanals.
Fibonacci-Fächer
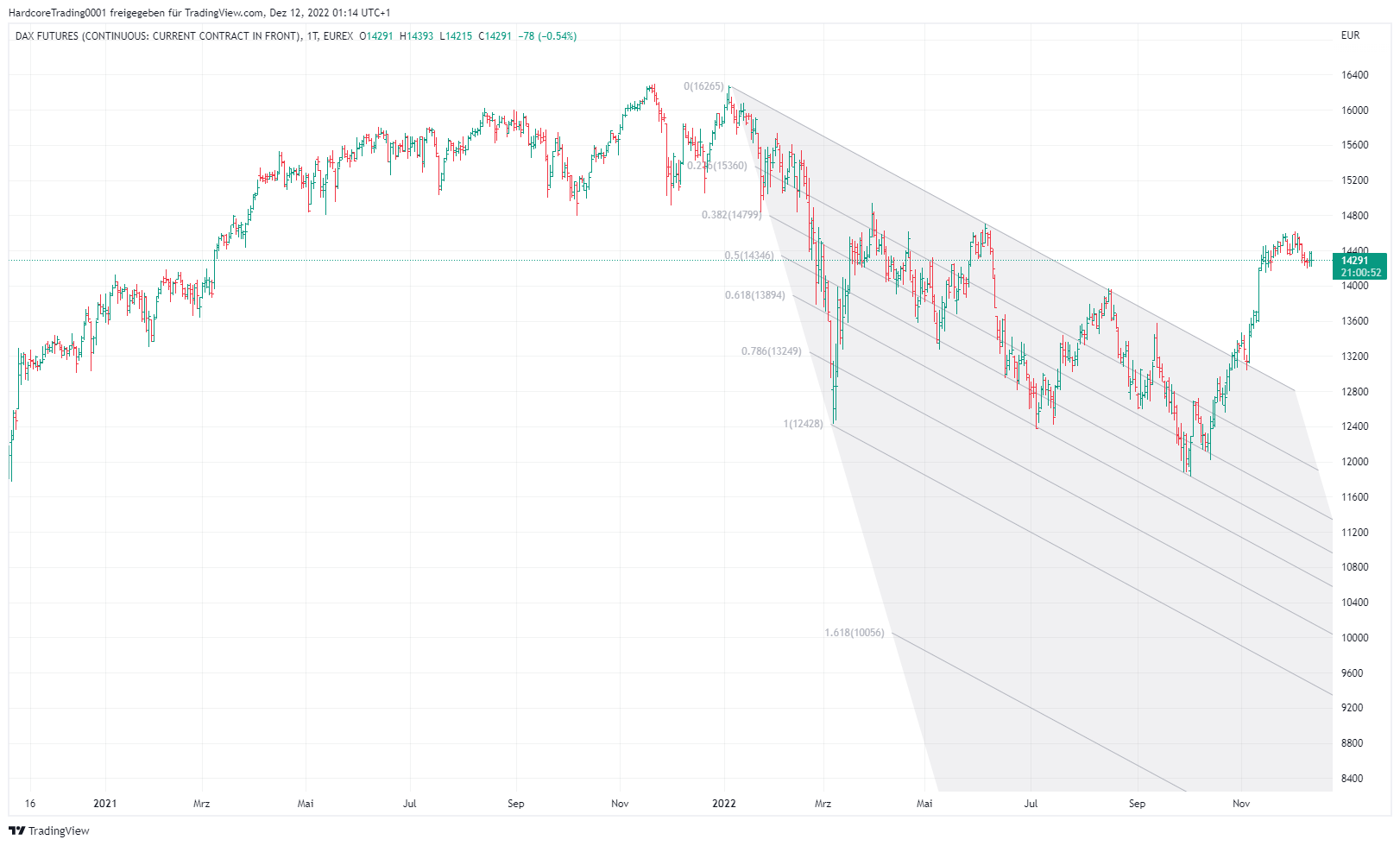
Fibonacci-Fächer werden nur selten zur Analyse von Preisdiagrammen verwendet, was recht überraschend ist, da es sich um ein sehr nützliches AT-Instrument handelt. Die Fibonacci-Fächer basieren auf Trendlinien. Bei der Messung einer langen Trendwelle werden mehrere andere Trendlinien mit unterschiedlichen Steigungen aufgezeichnet, die vom Ausgangspunkt des vorherrschenden Trends ausgehen.
Diese Linien markieren mögliche Unterstützungs- oder Widerstandsniveaus. Die am häufigsten verwendeten Fibo-Ratios in diesem Tool sind 38,2%, 50% und 61,8%. Fibonacci-Fächer sind ein etwas komplizierteres Instrument, da sie eine Methode darstellen, die sowohl Preis als auch Zeit kombiniert.
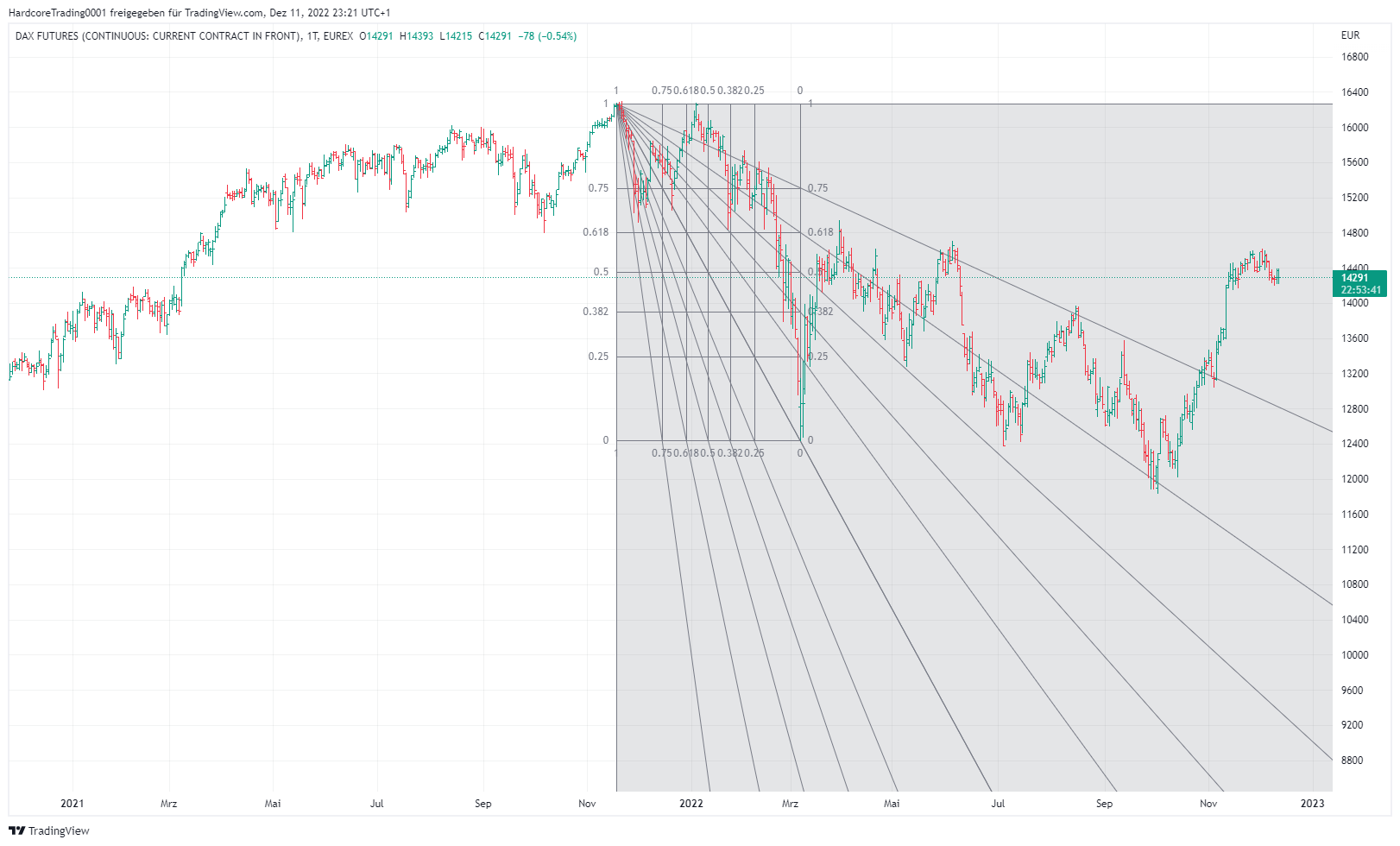
Fibonacci-Fächer folgen ebenfalls zwei aufeinanderfolgenden Hoch- und Tiefpunkten. Im Falle eines Aufwärtstrends und einem Hoch und einem Tief während eines Abwärtstrends. Auf diese Weise erhält man einen Fächer unterhalb des Trends nach oben und oberhalb des Trends nach unten, wie in der oberen Abbildung zu sehen ist.
Fibonacci-Bögen
Das letzte Fibonacci-Werkzeug sind die Fibo-Bögen. Standardmäßig zeichnet dieses Tool 7 Bögen in Bezug auf einen lokalen Höchst- oder Tiefstwert, die die Trendlinie zwischen diesem Extremwert und dem vorhergehenden entgegengesetzten Extremwert bei 38,2 %, 50 % und 61,8 % schneiden. Wie bei den Fibonacci-Fächern handelt es sich um ein Instrument, das sowohl die Frage nach dem Preis des Instruments als auch die Dauer der Preisbewegung kombiniert. Nachstehend finden Sie ein Beispiel für die Verwendung eines Fibonacci-Bogens.
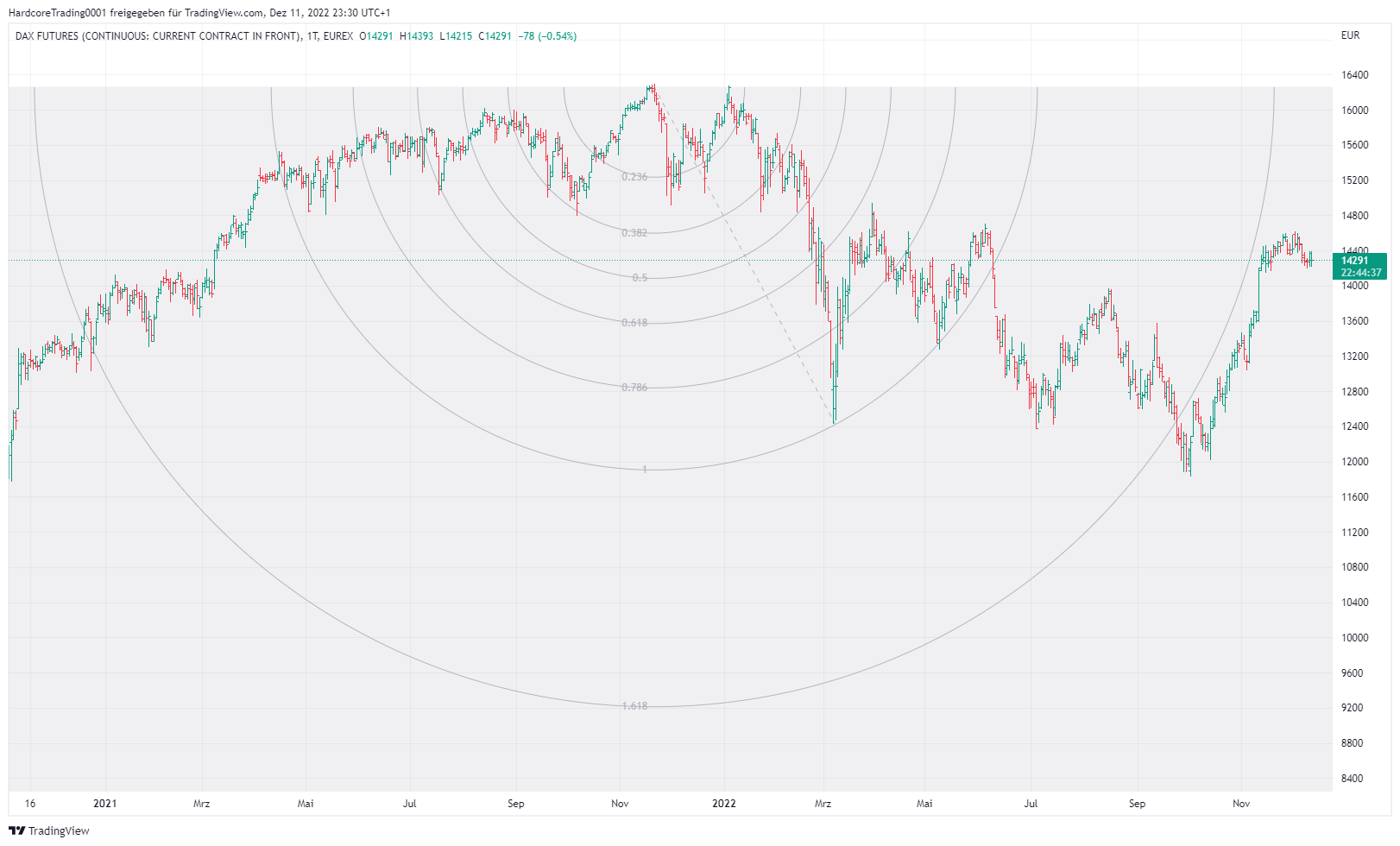
Fazit - warum Fibonacci-Techniken gerne verwendet werden
Die Beliebtheit der auf diesen Ratios basierenden technischen Analyseinstrumente ist darauf zurückzuführen, dass die Fibonacci-Methode eine der wenigen ist, die es erlaubt, mit hoher Wahrscheinlichkeit abzuschätzen, wo der Trend aufhören oder eine Korrektur beginnen wird. Natürlich gibt es keine Strategien, die eine 100- oder gar 90-prozentige Erfolgsquote aufweisen, aber auch hier helfen die Fibonacci-Ratios weiter.
Die hohe Genauigkeit ermöglicht es, relativ enge Absicherungsstops zu setzen. Dadurch wird das Verhältnis zwischen potenziellem Gewinn und eingegangenem Gesamtrisiko erheblich verbessert. Es ist jedoch wichtig zu wissen, dass geringe Verluste aus Fehlern, nur durch ein angemessenes Risikomanagement erreicht wird.
Ein übermäßiger Kapitaleinsatz bei einem Trade, kann zu großen Verlusten führen, was sich nicht nur auf Ihren Kontostand, sondern auch auf Ihre persönliche Meinung zum Handel an den Finanzmärkten negativ auswirken kann.
Die Integration von Fibonacci-Methoden in eigene Handelsstrategien ist sehr arbeitsintensiv und erfordert viel Erfahrung. Es reicht nicht aus, nur die Parameter einzustellen und sie auf ein Chart zu legen, wie es bei vielen Indikatoren und Oszillatoren der Fall ist.